Dijkstra's Algorithm

Quick Recap on Dijkstra's:

• no negative-weight edges
• weighted version of breadth-first-search
  • instead of FIFO queue, use priority queue
  • keys are shortest-path weights $d[v]$
• two sets of vertices
  • $S$ vertices whose final shortest-path weights are already found
  • $Q$ priority queue = vertices still in the queue, those we still need to evaluate their shortest path
• greedy-choice: at each step we choose the light edge

Code#

def init_single_source(vertices, source_node):
	for v in vertices:
		d[v] = inf
		p[v] = nil
	d[s] = 0
 
def relax(u, v, w):
	if d[v] > d[u] + w(u, v):
		d[v] = d[u] + w(u, v)
		p[v] = u
 
def dijkstra(V, E, w, s):
	init_single_source(V, s):
	S = set() # init empty
	Q = priority_queue(V)
 
	while Q is not empty:
		u = extract_min(Q)
		S = S.add(u)
		for v in adj_list[u]:
			relax(u, v, w)

Mathematical Context For Path Properties#

First, let's cover the working parts & properties:

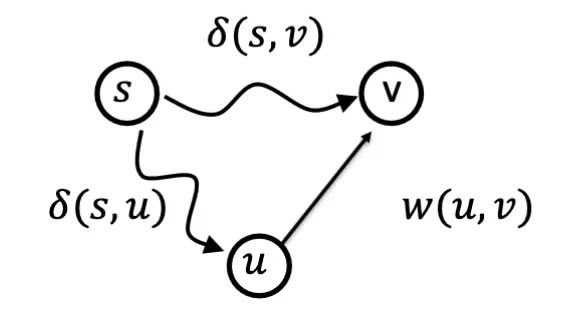
Triangle Inequality#

The Triangle Inequality states that for all $(u,v)\in E$, we have $\delta(s,v) \leq \delta(s,u)+w(u,v)$.

Proof#

• we have a path $s\leadsto u\to v$, as well as a shortest path $s\leadsto v$
  • the weight of the shortest path $s\leadsto v$ is $\leq$ any path $s\leadsto v$
• let us say that the path $s\leadsto u=\delta(s,u)$
• this means if we use the shortest path $s\leadsto u$ and direct edge $u\to v$, then the weight along $s\leadsto u\to v=\delta(s,u)+w(u,v)$

Upper Bound Property#

The Upper Bound Property states that we always have $d[v]\geq\delta(s,v),\forall v\in V$. Once $d[v]=\delta(s,v)$, it never changes.

Proof by Contradiction on Inequality#

• let's assume this starts initially true
• then, assume $\exists v\in V;d[v]<\delta(s,v)$
  • this is the first instance of it happening

We know that this can't have happened at initialization, because init_single_source() sets all $d[v]=\infty$, therefore this must have happened at some point during the algorithm's run time.

Let $u$ be the vertex that causes $d[v]$ to change, since in order for us to have altered $d[v]$, relax(u, v, w) must have been called.

Within relax(u, v, w), $d[v]$ is altered only if:

• d[v] > d[u] + w(u,v) evaluates to true.
• if so, d[v] = d[u] + w(u, v) is the change made to $d[v]$

Recall our initial assumption, we have: $d[v]<\delta(s,v)$

1. via Triangle Inequality, $\delta(s,v)\leq\delta(s,u)+w(u,v)$
2. $d(s,u)\leq d[u]$, since $v$ was the first vertex where its estimate was less than the shortest path, meaning:
   • $\delta(s,u)\leq d[u]\implies \delta(s,u)+w(u,v)\leq d[u]+w(u,v)$
3. this results in the full inequality:

However, this is impossible, since relax(u, v, w) set $d[v]=d[u]+w(u,v)$, and nothing can be equal and be explicitly less than something else simultaneously.

Thus, we have proved $\delta(s,v)\leq d[v],\forall v\in V$. $\blacksquare$

No-Path Property#

The No-Path Property states that if $\delta(s,v)=\infty$, then $d[v]$ will always equal $\infty$

Proof#

• via the Upper Bound Property, $d[v]\geq\delta(s,v)$
• this means $\delta(s,v)=\infty \implies d[v]=\infty$

$\blacksquare$

Convergence Property#

The Convergence Property states that if:

1. we have a path $s\leadsto u\to v=\delta(s,v)$ – (it is a shortest path)
2. $d[u]=\delta(s,u)$
3. we call relax(u, v, w),

then $d[v]=\delta(s,v)$ afterward.

Proof#

We relax $v$ within this code:

if d[v] > d[u] + w(u, v):
	d[v] = d[u] + w(u, v)
	p[v] = u

After this code, $d[v]\leq d[u]+w(u,v)$, because when entering relax(u, v, w):

1. if $d[v]$ was $\leq d[u]+w(u,v)$ – we would bypass the if-condition, and nothing happens
2. if $d[v]$ was $>$, then it is set $=d[u]+w(u,v)$

The only two cases resulting in $d[v]\leq d[u]+w(u,v)$.

We can take the RHS and simplify it, as we have defined $d[u]=\delta(s,u)$:

Since we defined $s\leadsto u\to v$ to be a shortest path, meaning:

Finally, by the Upper Bound Property, we know that $d[v]\geq \delta(s,v)$. This means we must have $d[v]=\delta(s,v)$. $\blacksquare$

Path Relaxation Property#

Let $p = \langle v_{0},v_{1},\dots,v_{k} \rangle$ be a shortest path from $s=v_{0}$ to $v_{k}$. Relaxing these edges, in order, will ensure that $d[v_{k}]=\delta(v_{0},v_{k})$. (The shortest path estimate at $v_{k}$ is the correct one).

Proof by Induction#

We will show via induction on the number of vertices that $d[v_{i}]=\delta(s,v_{i})$ after the edge $(v_{i-1},v_{i})$ is relaxed.

Base Case: $i=0$, and $v_{0}=s$.

At initialization in init_single_source(), we set $d[s]=0\implies\delta(s,s)=0$.

Inductive Step: Assume $d[v_{i-1}]=\delta(v_{i-1}, s)$.

As we relax edge $(v_{i-1},v_{i})$, note that we have met the pre-conditions for the Convergence Property:

1. we have a shortest path $s\leadsto v_{i-1} \to v_{i} \leadsto v_{k}$
   • by optimal substructure, the path $s\leadsto v_{i-1} \to v_{i}$ must also be a shortest path $\delta(s,v_{i})$
2. we have $d[v_{i-1}]=\delta(v_{i-1},s)$
3. we are now calling relax on $(v_{i-1},v_{i})$

hence, $d[v_{i}]$ converges to be $\delta(v_{i},s)$ and never changes.

We have proved by induction that $d[v_{k}]=\delta(v_{0},v_{k})$ if we relax the edges in order. $\blacksquare$

Dijkstra's Proof#

via Loop Invariant#

We will prove via a Loop Invariant that Dijkstra's Algorithm is correct.

def dijkstra(V, E, w, s):
	init_single_source(V, s):
	S = set() # init empty
	Q = priority_queue(V)
 
	while Q is not empty:
		u = extract_min(Q)
		S.add(u)
		for v in adj_list[u]:
			relax(u, v, w)

Loop Invariant: At the end of each iteration of the while loop, $d[v]=\delta(s,v), \forall v\in S$

Initialization#

At initialization, $S$ is an empty set, and so the loop invariant holds as a by-product of having no $v\in S$ yet.

Maintenance#

Show that $d[v] = \delta(s,v)$ when $v$ is added to $S$ in each iteration.

We will prove the maintenance property through contradiction:

Assume that for the first time, after an iteration on some vertex $v$, we have added $v$ to $S$, and $d[v]\neq\delta(s,v)$.

What do we know?

For starters, we know that $v\neq s$, as $d[s]=\delta(s,s)=0$. This means that $s\in S$ and $S\neq \emptyset$ when $v$ is added.

We also know, by the No-Path Property, there exists some path $s\leadsto v$. Otherwise, the property states that:

which contradicts our assumption that $d[v]\neq\delta(s,v)$.

Since there exists a path $s\leadsto v$, there must exist a shortest path, $p$, from $s\leadsto v$.

Allow us to decompose $p$ into $s\leadsto^{p_{1}} x\to y\leadsto^{p_{2}}v$, such that $\{ s,x \}\in S$, $\{ y,v \}\in Q$, and edge $(x,y)$ is the edge crossing the two sets $S,Q$.

Claim: $d[y]=\delta(y,s)$ when $u$ is added to $S$

Proof:

1. by optimal substructure, any subpath within $s\leadsto v$, such as $s\leadsto x\to y$, is a shortest path as well
2. $x\in S \implies d[x] = \delta(s,x)$
3. we called relax on edge $(x,y)$ at the time of adding $x$ to $S$
   • so by the Convergence Property, $d[y]=\delta(s,y)$

This means that if $y=v$, we have already reached a contradiction, as our initial assumption was:

and we have just proved that the estimate is the correct delta, and the proof is finished.

However, what if $y\neq v$? Can we still reach a contradiction?

Once again, we know that there exists a shortest path $p$ from $s\leadsto v$ via the No-Path Property, and that any subpath along $p$ is also a shortest path by optimal substructure. This implies a chain of logic:

1. $s\leadsto y$ is a shortest path
2. by our Claim, $d[y]=\delta(s,y)$
3. since there are no non-negative edge weights, a shortest path $s\leadsto y\leadsto v$ must be at least as long as $\delta(s,y)$, meaning:
4. $s\leadsto y\leadsto v\implies\delta(s,y)\leq\delta(s,v)$
   • this is because we must pass $y$ to get to $v$
5. $\delta(s,v)\leq d[v]$ by the Upper Bound Property

Putting this all together:

Lastly, we know that:

• we are in the iteration of the while loop where we choose $v$
• $Q$ stores a vertex $v$ as a key-value pair { v : d[v] }
• extract_min(Q) chooses to extract the vertex v if d[v] is minimum across all estimates it finds in Q
• both $v$ and $y$ were in $Q$ when we chose $v$

This means in order for $v$ to have been chosen, $d[v]\leq d[y]$. We can conclude:

The estimate $d[v]$ must be equal to the estimate $d[y]$ if it is both $\leq$ and $\geq$ $d[y]$. This, again, contradicts our initial assumption that $d[v]\neq\delta(s,v)$ as $d[v]=d[y]$, and $d[y]=\delta(s,y)$ by our initial Claim. $\blacksquare$

Termination#

At the end of the while loop, $Q$ (which was equal to $V$) is now the $\emptyset$. At each iteration, we added the current vertex to $S$, meaning that now, $S=V$. This implies that:

The loop variant has been shown to hold across initialization, maintenance, and termination, thus proving Dijkstra's Algorithm. $\blacksquare$